Learning Attention-based Embeddings for Relation Prediction in Knowledge Graphs 논문 리뷰

Learning Attention-based Embeddings for Relation Prediction in Knowledge Graphs

• KBAT 논문에 대한 해석 및 정리입니다.
• 현재 relation prediction (knoledge graph completion)에서 가장 좋은 성능을 보이는 모델입니다.
• KBAT는 지식 그래프에 attention embedding을 적용한 모델입니다.

Introduction

  Relation prediction(knowledge base completion)에서 state-of-the-art 모델은 대부분 knoledge embedding 기반 모델이다. 크게 translational 모델과 convolutional neural network 모델로 나눌 수 있다. translational model은 간단한 연산과 제한된 parameter를 사용해 임베딩을 학습한다. 따라서 낮은 수준의 임베딩을 생성한다. 반대로 CNN 기반 모델은 parameter의 효율성과 더 복잡한 관계를 고려하는 특성 때문에 더 풍부한 임베딩을 학습한다. 그러나 두 종류의 모델 모두 각각의 트리플을 독립적으로 고려하기 때문에 주어진 개체 근처에 내재된 관계를 포착하지 못하는 단점이 있다.
  앞서 언급한 관찰에 의거하여 이 논문에서는 relation prediction을 위한 일반화된 attention 기반 그래프 임베딩 기법을 제안한다. node classification에서 graph attention networks(GATs)는 그래프의 가장 관련성있는 부분인 1-hop 이웃의 node feature에 집중하였다. 이 논문은 attention mechanism을 일반화하고 확장시켜 주어진 개체(node)의 multi-hop 이웃 안에 있는 개체(node)와 관계(edge) 모두에 attention을 적용한다.
  논문에서 제시한 아이디어는 다음과 같다.

1. 주어진 node 주변의 multi-hop 관계를 포착한다.
2. 여러 관계에서 개체가 수행하는 역할의 다양성을 캡슐화한다.
3. 의미적으로 유사한 관계 클러스터에 존재하는 기존 지식을 통합한다.

그러나 모델이 깊어질수록 거리가 먼 개체의 영향은 기하급수적으로 줄어든다. 이를 해결하기 위해 n-hop 이웃 사이에 auxiliary edge를 도입하여 개체 간 지식 흐름을 용이하게 한다. 논문에서는 새로운 generalized graph attention model과 ConvKB가 encoder, decoder로 동작하는 encoder-decoder 모델을 제안한다.
  이 논문은 지식그래프에서 relation prediction을 위한 graph attention based embedding을 최초로 제안한다. graph attention mechanism 일반화하고 확장하여 주어진 개체의 multi-hop 이웃에 존재하는 개체와 관계 feature를 동시에 포착한다. 모델을 다양한 실제 dataset을 사용해 까다로운 relation prediction task에 대해 평가한다.

Related Work

  최근에 relation prediction을 위한 다양한 지식 그래프 임베딩이 제안되고 있다. 이것들은 크게 compositional, translational, CNN based, graph based 모델로 나눌 수 있다. 앞의 세 종류의 모델은 생략하고 graph based 모델에 대해서만 설명하려 한다. graph based 모델 중 R-GCN이 존재한다. 이것은 graph convolutional networks(GCNs)를 관계 data에 대해서도 적용하도록 확장한 것이다. 개체의 이웃에 대해서 convolution 연산을 적용하고 이를 같은 weight로 할당한다. 그러나 CNN based 모델보다 성능이 좋지 않다.
  주어진 예시들은 개체 feature만 집중하거나 개체와 관계를 분리하여 지식그래프 embedding을 학습한다. 논문이 제안한 모델은 multi-hop과 주어진 개체의 n-hop 이웃에서 의미적으로 유사한 관계를 전체적으로 포착한다.

Our Approach

Graph Attention Networks (GATs)

  Graph convolutional networks (GCNs)는 개체의 이웃에서 정보를 모으고 이를 동일한 가중치로 전달한다. GATs는 GCN과 달리 node의 이웃에 대해 중요도를 다르게 할당하여 학습한다.   layer로 node의 입력 집합은 \(\text{x}= \{ \overrightarrow{x}_1,\overrightarrow{x}_2,\dotsb ,\overrightarrow{x}_N\}\)이다. layer는 node feature의 집합을 벡터 \(\text{x}^\prime= \{ \overrightarrow{x}^\prime_1,\overrightarrow{x}^\prime_2,\dotsb ,\overrightarrow{x}^\prime_N\}\)로 변환한다. 여기서 \(\overrightarrow{x}_i, \overrightarrow{x}^\prime_i\)는 개체 \(e_i\)의 입력과 출력 embedding이고 \(N\)은 개체(node)의 수이다. 하나의 GAT layer는 \(e_{ij}=a(\text{W}\overrightarrow{x}_i,\text{W}\overrightarrow{x}_j)\)로 표현할 수 있다. \(e_{ij}\)는 그래프 \(\mathcal{G}\)에 있는 edge \((e_i,e_j)\)의 attention value이다. \(\text{W}\)는 입력 feature를 높은 차원의 출력 feature로 선형변환하기 위한 parameter이다. \(a\)는 임의로 선택한 attention function이다.
  각 edge가 갖는 attention value는 source node \(e_i\)에 대한 edge\((e_i,e_j)^\prime\) feature의 중요도이다. relative attention \(\alpha_{ij}\)는 모든 이웃 값에 대해서 softmax function을 사용해 계산한다. 아래는 layer의 출력을 나타낸다.
\(\overrightarrow{x}^\prime_i=\sigma(\sum_{j\in\mathcal{N}_i}\alpha_{ij}\text{W}\overrightarrow{x}_j)\)
GAT은 학습 과정을 안정화하기 위해 multi-head attention을 사용한다. K개의 attention head를 concatenate하는 multihead attention process는 다음과 같이 수행된다. \(\overrightarrow{x}^\prime_i=\|^K_{k=1}\sigma(\sum_{j\in\mathcal{N}_i}\alpha_{ij}^k\text{W}^k\overrightarrow{x}_j)\)
\(\|\)는 concatenation을 의미하고, \(\sigma\)는 non-linear function을 나타낸다. \(\alpha_{ij}^k\)는 k번째 attention mechanism에서 계산된 edge \((e_i,e_j)\)의 attention 계수를 나타낸다. \(\text{W}^k\)는 k번째 attention mechanism에서 linear transformation matrix를 나타낸다. 마지막 layer에서 embedding 출력은 평균을 사용하여 multi-head attention을 얻는다.
\(\overrightarrow{x}^\prime_i=\sigma(\frac{1}{K}\sum_{k=1}^K\sum_{j\in\mathcal{N}_i}\alpha_{ij}^k\text{W}^k\overrightarrow{x}_j)\)

Relations are Important

  GATs는 지식그래프에서 중요한 부분인 관계(edge) feature를 무시하기 때문에 부적절하다. 지식그래프에서 개체는 그들이 속한 relation에 따라 다양한 역할을 가진다. 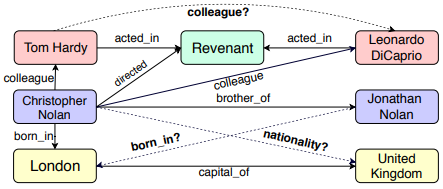예를 들어 그림 1에서 개체 “Christopher Nolan”은 “brother”, “director”의 역할로 두개의 다른 트리플에서 나타난다. attention mechanism에서 관계와 이웃 node feature를 모두 사용하는 새로운 embedding 접근을 제안한다. 모델에서 building block이 되는 single attention layer를 정의한다. GAT와 유사하게 이 framework는 attention mechanism의 특정 선택과 무관하다.
  모델의 각 layer에서는 입력으로 두개의 embedding matrix를 가진다. entity embedding은 행렬 \(\text{H}\in\Bbb R^{N_e \times T}\)로 표현된다. i번째 행은 개체 \(e_i\)의 embedding이고, \(N_e\)는 개체의 수, \(T\)는 각 개체 embedding의 feature 차원이다. 이와 비슷하게 관계 embedding 또한 행렬 \(\text{G}\in\Bbb R^{N_r \times P}\)로 표현된다. layer는 \(\text{H}^\prime\in\Bbb R^{N_e \times T^\prime},\ \text{G}^\prime\in\Bbb R^{N_r \times P^\prime}\)을 출력한다.
  개체 \(e_i\)에 대한 새로운 embbeding을 얻기 위해 \(e_i\)가 속한 모든 트리플 표현을 학습한다. 트리플 \(t^k_{ij}=(e_i,r_k,e_j)\)에 해당하는 개체와 관계 feature 벡터를 concatenate하고 선형 변환을 거쳐 이 embedding을 구한다.
\(\overrightarrow{c}_{ijk} = \text{W}_1 |\overrightarrow{h_i}| |\overrightarrow{h_j}| |\overrightarrow{g_k}|\)
\(\overrightarrow{c}_{ijk}\)는 트리플 \(t_{ij}^k\)의 벡터 표현이다. 벡터 \(\overrightarrow{h_i}, \overrightarrow{h_j}, \overrightarrow{g_k}\)는 각각 개체와 관계 embedding \(e_i, e_j, r_k\)를 나타낸다. \(\text{W}_1\)은 선형 변환 행렬을 나타낸다. 각각의 트리플 \(t^k_{ij}\)의 중요도를 학습한 값을 \(b_{ijk}\)로 나타낸다. weight matrix \(\text{W}_2\)를 parameter로 갖는 선형 변환을 수행하고, LeakryRelu의 non-linearity를 사용해 absolute attention value를 얻는다.
\(b_{ijk}=\text{LeakyReLU}(\text{W}_2c_{ijk})\)
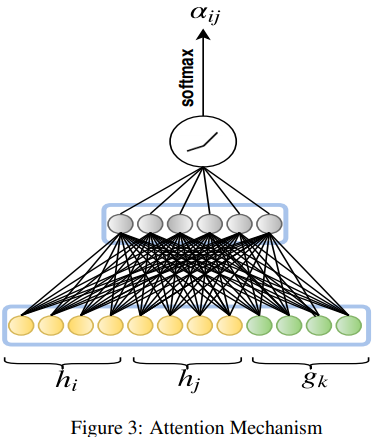relative attention value를 얻기 위해 softmax를 \(b_{ijk}\)에 적용한다. 그림 2는 하나의 트리플에 대한 relative attention value \(\alpha_{ijk}\)를 얻는 과정을 보여준다.
\(\alpha_{ijk}=\text{softmax}_{jk}(b_{ijk})\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\=\frac{\text{exp}(b_{ijk})}{\sum_{n\in\mathcal{N}_i}\sum_{r\in\mathcal{R}_{in}}\text{exp}(b_{inr})}\)
\(\mathcal{N}_i\)는 \(e_i\)의 이웃을 의미하고 \(\mathcal{R}_{in}\)는 \(e_i, e_j\)와 연결된 관계 집합을 의미한다. \(e_i\)의 새로운 embedding은 각각 트리플의 표현에 relative attention value를 곱한 값을 모두 합쳐 얻을 수 있다.
\(\overrightarrow{h_i^\prime}=\sigma\left(\sum_{j\in\mathcal{N}_i} \sum_{k\in\mathcal{R}_{ij}} \alpha_{ijk} \overrightarrow{c}_{ijk}\right)\) multi-head attnetion은 학습 과정을 안정화하고, 이웃으로부터 더 많은 정보를 캡슐화한다. M개의 독립된 attention mechanism은 embedding을 계산하고 concatenate한다.
\(\overrightarrow{h_i^\prime}=\|^M_{m=1}\sigma\left(\sum_{j\in\mathcal{N}_i} \alpha_{ijk}^m c_{ijk}^m)\right)\)

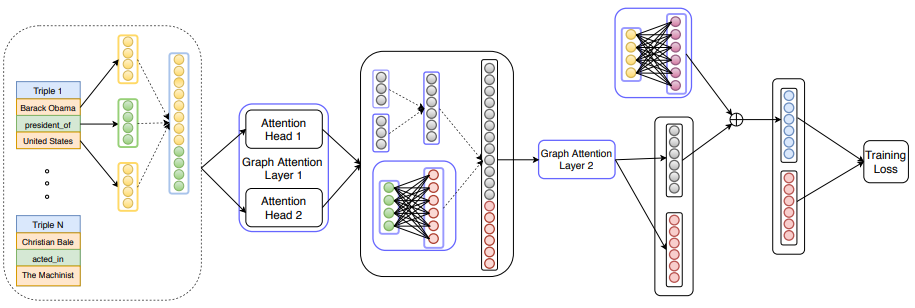
그림3: 점선은 concatenate 연산을 나타낸다. 초록원은 관계 embedding 벡터, 노란원은 개체 embedding 벡터를 나타낸다.

그림 3은 graph attention layer를 보여준다. graph attention layer 1을 거친 후 관계 embedding에 선형 변환을 하여 추가해준다. final attentional layer에서 multiple head에서 나온 embedding을 concatenate 하는 대신 평균을 적용해 최종 embedding vector를 얻는다.
\(\overrightarrow{h_i^\prime}=\sigma\left(\frac{1}{M}\sum_{m=1}^M\sum_{j\in\mathcal{N}_i} \sum_{k\in\mathcal{R}_{ij}} \alpha_{ijk}^m c_{ijk}^m\right)\)
그러나 embedding을 학습하는 과정에서 개체는 처음에 갖고 있던 embedding 정보를 잃는다. 이를 해결하기 위해 초기 embedding 벡터에 최종 개체 embedding의 dimension 크기만큼 선형 변환을 한 후, 그 값을 최종 embedding vector에 더해준다. 논문의 구조는 두 개체 사이의 n-hop 이웃에 대한 auxiliary relation을 도입하여 edge의 개념을 directed path로 확장한다. auxiliary relation의 embedding은 경로에 있는 모든 관계 embedding의 합이다. 이 모델은 반복적으로 개체의 먼 이웃으로부터 지식을 모은다.
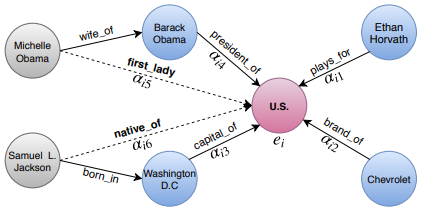그림 4에서 나타나듯이 모델의 첫번째 layer에서 모든 개체는 직접 유입되는 이웃으로 부터 정보를 얻는다. 두번째 layer에서 ‘U.S’는 이전 layer에서 이웃 인 ‘Michelle Obama’와 ‘Samuel L. Jackson’에 대한 정보를 이미 가지고있는 ‘Barack Obama’, ‘Ethan Horvath’, ‘Chevrolet’, ‘Washington D.C’ 개체로부터 정보를 얻는다. 일반적으로 n layer 모델에서 들어오는 정보는 n-hop 이웃에 축적된다. 새로운 embedding을 학습하는 과정과 n-hop 이웃간 auxiliary edge를 소개하는 전체 과정이 그림 4에 나타나있다. 각 iteration마다 모든 GAT layer 이후와 첫번째 layer 이전에 개체 embedding을 정규화 한다.

Training Objective

  이 모델의 score function은 TransE의 score function에서 아이디어를 가져왔다. 주어진 참 트리플 \(t^k_{ij}=(e_i, r_k,e_j)\)에서 \(e_i\)에서 \(r_k\)로 연결된 가장 가까운 이웃이 \(e_j\)가 되도록 embedding 한다. 특히 \(d_{t_{ij}}=\|\overrightarrow{h_i}+\overrightarrow{g_k}-\overrightarrow{h_j}\|_1\) 다음과 같은 L1-norm dissimilarity를 최소화하도록 개체와 관계 embedding을 학습한다.
  모델을 학습시키는데 hinge-loss를 사용하였다. \(L(\Omega)=\sum_{t_{ij}\in S}\sum_{t_{ij}^\prime\in S^\prime} \text{max} \{ d_{t_{ij}}^\prime-d_{t_{ij}}+\gamma,0 \}\) 여기서 \(\gamma>0\)은 margin hyper-parameter이고 \(S\)는 valid 트리플, \(S^\prime\)은 invalid 트리플이다.

Decoder

  decoder로는 ConvKB 모델을 사용했다. convolution layer에서는 각 차원에 걸쳐 트리플의 global embedding properties를 분석하고, 논문 모델의 transitional characteristic을 일반화한다. ConvKB의 구조는 다음 그림과 같다. 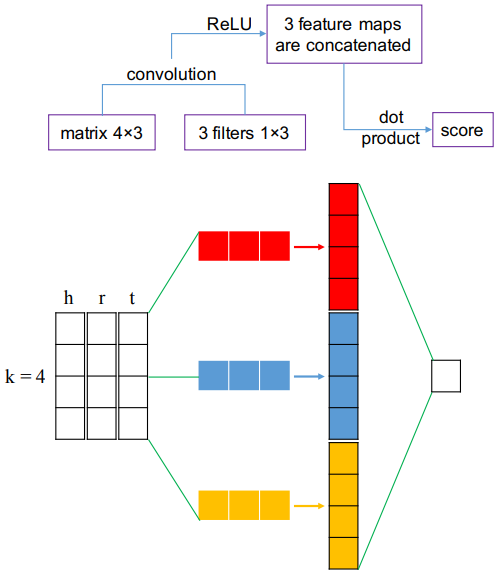여러 feature map을 사용하는 score function은 다음과 같다. \(f(t_{ij}^k)=\left( \|^\Omega_{m=1}\text{ReLU}([\overrightarrow{h_i},\overrightarrow{g_k},\overrightarrow{h_j}]\ast\omega^m) \right)\cdot\text{W}\)
\(\omega^m\)는 \(m\)번째 convolution filter, \(\Omega\)는 filter의 숫자, \(\ast\)는 convolution 연산, \(\text{W}\in\Bbb R^{\Omega k\times1}\)은 최종 점수를 얻기 위한 선형 변환에 사용되는 행렬을 뜻한다. 모델은 soft-margin loss를 사용해 학습한다.
\(\mathcal{L}=\sum_{t_{ij}^k\in\left\{S\cup S^\prime\right\}}\text{log}(1+\text{exp}(l_{t_{ij}^k}\cdot f(t_{ij}^k)))+\frac{\lambda}{2}\|\text{W}\|^2_2\)
\(l_{t_{ij}^k}=\begin{cases}1 & \text{for}\ t_{ij}^k\in S\\-1 & \text{for}\ t_{ij}^k\in S^\prime\end{cases}\)

Experiments and Results

Datasets

  평가를 위해 WN18RR, FB15k-237, NELL-995, Unified Medical Language Systems(UMLS), Alyawarra Kinship dataset을 사용했다. 다음은 사용된 dataset의 정보이다.

Dataset	# Entities	# Relations	# Train	# Valid	# Test	# Total	# Mean in-degree	# Median in-degree
WN18RR	40,943	11	86,835	3034	3134	93,0003	2.12	1
FB15k-237	14,541	237	272,115	17,535	20,466	310,116	18.71	8
NELL-995	75,492	200	149,678	543	3992	154,213	1.98	0
Kinship	104	25	8544	1068	1074	10,686	82.15	82.5
UMLS	135	46	5216	652	661	6529	38.63	20

Training Protocol

  head와 tail 개체를 교체하는 방식으로 두 개의 invalid triple을 만든다. TransE에서 생성된 개체와 관계 embedding을 초기 embedding으로 사용했다. 학습 과정을 두단계로 나누었다. 먼저 GAT을 학습시켜 graph의 개체와 관계 정보를 인코딩한다. 그 후 decoder 모델을 학습시켜 relation prediction task를 수행한다. Adam optimizer를 사용하였고, 개체와 관계 embedding의 final layer는 200으로 설정했다.

Evaluation Protocol

  Relation prediction task에서는 트리플 \((e_i,r_k,e_j)\)에서 \(e_i\) 또는 \(e_j\)가 빠졌을 때 이를 예측하는 것이다. 이전 연구와 마찬가지로 filtered setting을 사용했다. 평가에는 MRR, MR, Hits@N을 사용했다.

Results and Analysis

  아래 그림에 실험 결과를 나타냈다. 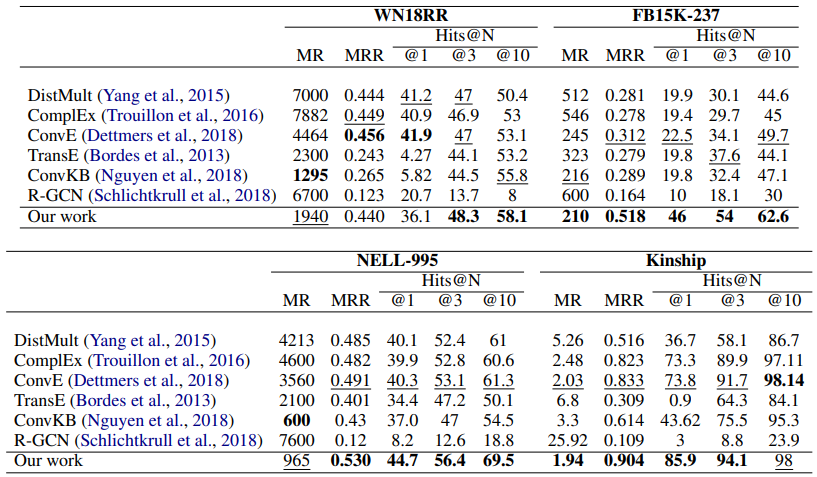KBAT 모델이 뛰어난 성능 향상을 보였다는 것을 알 수 있다.
Attention Values vs Epochs: 특정 노드에서 epoch이 증가함에 따른 attention 분포를 연구했다. 아래 그림은 FB15k-237에서의 attention 분포이다. 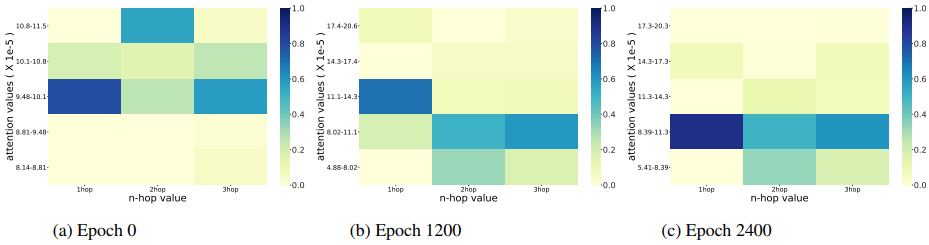학습 초기에는 attention이 random으로 분포되어 있다. 학습이 진행되면서 모델이 이웃으로부터 더 많은 정보를 모아감에 따라 먼 이웃보다 가까운 이웃에 더 많은 가중치를 둔다. 모델이 수렴되면 node의 n-hop 이웃에서 multi-hop 및 클러스터링된 관계 정보를 수집하는 방법을 배운다.
PageRank Analysis: 논문에서는 개체들 사이의 복잡하고 숨겨진 multi-hop 관계가 sparse graph보다 dense graph에서 더 잘 포착된다고 주장한다. 이를 증명하기 위해 ConvE와 유사하게 PageRank와 MRR의 상관관계를 실험했다.

Dataset	PageRank	Relative Increase
NELL-995	1.32	0.025
WN18RR	2.44	-0.01
FB15k-237	6.87	0.237
UMLS	740	0.247
Kinship	961	0.388

이 표에서 Relative Increase는 DistMult와 비교했을때 MRR의 증가량이다. PageRank가 증가함에 따라 MRR도 증가했음을 알 수 있다. NELL-995와 WN18RR을 비교하면 오류가 관찰되는데 이는 WN18RR의 sparse하고 hierarchical한 구조 때문이다. 이는 하향식 재귀 방식으로 정보를 수집하지 않는 모델의 특성 때문으로 보인다.

Ablation Study

  모델에서 n-hop 정보를 제거한 path generalization(-PG) 또는 relation Information(-Relations)을 제외했을때 MR을 분석했다. 아래 그림은 NELL-995에서 모델들의 epoch에 따른 MR 변화를 나타낸다. 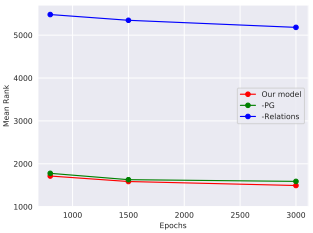Relation을 제거했을 때 큰 폭으로 성능이 떨어지는 것을 보아 relation embedding이 중요한 역할을 하는 것을 알 수 있다.

Conclusion and Future Work

  본 논문에서는 주어진 개체에 대해 multi-hop 이웃의 개체와 관계 feature를 포착하는 graph attention mechanism을 제안했다. 향후 연구로는 모델이 hierarchical graph에서 더 잘 수행하도록 확장하고, graph attention 모델에서 개체간 higher-order relation을 더 잘 포착하도록 할 계획이다.