Adaptive Convolution for Multi-Relational Learning 논문 리뷰

Adaptive Convolution for Multi-Relational Learning

• ConvR 논문에 대한 해석 및 정리입니다.

Introduction

  ConvE는 입력 개체와 관계의 상호작용을 포착하기에는 불충분하다. ConvE는 입력 개체와 관계를 단순히 결합해 convolution layer의 입력으로 사용했다. 또한 global filter를 사용하는 2D convolution은 concatenate line에서만 입력 개체와 관계의 상호작용을 얻을 수 있다.

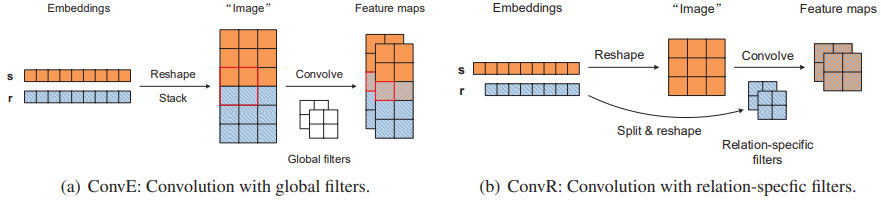
그림1: ConvE와 ConvR이 reshape, convolution 된다. 오렌지색은 개체, 파란색은 관계를 나타낸다. 흰색 블럭은 입력 개체와 관계에 적용되는 global filter이다.

그림 1(a)는 3x3 크기의 두 행렬을 reshape, stack하여 convolution layer에 입력한다. 입력을 2x2 크기의 global filter로 연산하면 두 행렬이 인접한 부분에서만 상호작용이 일어난다. 이로 인해 output convolutional features의 아주 작은 부분에서만 개체와 관계의 상호작용을 포착한다. 대다수의 개체와 관계는 독립적으로 계산된다. (그림 1(a)에서는 파란색과 오렌지색으로 빗금쳐진 20% 범위에서만 일어난다.)
  이 논문에서는 입력 개체와 관계 사이의 상호작용을 최대화하는데 초점을 두었다. 그림1(b)는 ConvR의 핵심 아이디어를 나타낸다. 이 모델의 핵심 아이디어는 관계에 대해 적응적으로(adaptively) 구성된 필터를 사용하여 개체의 convolution을 용이하게 하는 것이다. 관계로 구성된 filter를 사용하는 adaptive convolution으로 개체의 상호작용을 많이 포착하도록 한다. 트리플이 주어지면 주어 개체를 나타내는 벡터는 convolution layer의 입력으로, 관계를 나타내는 벡터는 filter로 설정된다. 이 방식은 생성된 모든 feature가 개체와 관계의 상호작용을 포착할 수 있다(그림 1(b)에서 파란색과 오렌지색으로 빗금쳐진 부분). 이 convolution feature는 마지막으로 목적어 개체와 projected, matched 된다.
  Adapdive convolution을 사용하면 parameter 측면에서 효율적인 모델을 구성할 수 있다. 그림 1의 두 모델을 비교하면 ConvR은 global filter가 필요하지 않고, ConvE의 것보다 반 정도 작은 feature map을 생성한다. adaptive convolution 아이디어는 2D convolution에 국한되지 않고, 1D 또는 3D로 쉽게 확장 가능하다. 다만 ConvE와의 비교를 용이하게 하기 위해 이 논문은 2D convolution을 사용해 ConvR의 우수성을 보인다.

Background

앞에서 작성한 ConvE 논문의 Related Work와 큰 차이가 없어 생략하겠습니다.
ConvE 논문 ConvE 논문 리뷰 Related Work

Adaptive Convolution on Multi-relational Data

The ConvR model

  주어진 트리플 \((s,r,o)\)에 대해 ConvR은 두 개체 \(s,o\)를 벡터 \(\text{s,o}\in \mathcal(R)^{d_e}\), 관계 \(r\)을 벡터 \(\text{r} \in \mathcal(R)^{d_r}\)로 변환했다. 여기서 \(d_e,d_r\)은 개체와 관계의 embedding size이다. 주어 개체 벡터는 2D 행렬 \(\text{S}\in \Bbb R^{d_e^h \times d_e^w}\)(\(d_e = d_e^hd_e^w\))로 변환되고 convolution layer의 입력으로 주어진다. ConvE 논문에서 보인 것처럼 2D convolution이 1D보다 더 많은 feature를 추출할 수 있어 모델의 표현력을 높인다. 관계 벡터 \(\text{r}\)은 모두 같은 크기로 나뉜다(\(\text{r}^{(1)},\dotsb,\text{r}^{(c)}\)). 각각의 벡터 \(\text{r}^{(l)}\in \Bbb R^{d_r/c}\)는 2D convolution의 필터로 변환된다(\(\text{R}^{(l)}\in \Bbb R^{h \times w}\)). 여기서 \(c\)는 filter의 크기, \(h,w\)는 각 필터의 가로와 세로이고 \(d_r=chw\)이다. 위 그림 1(b)에서는 길이가 9인 주어 개체 벡터가 3x3행렬로 변환되고, 길이가 8인 관계 벡터가 두개의 2x2 필터로 변환된다.
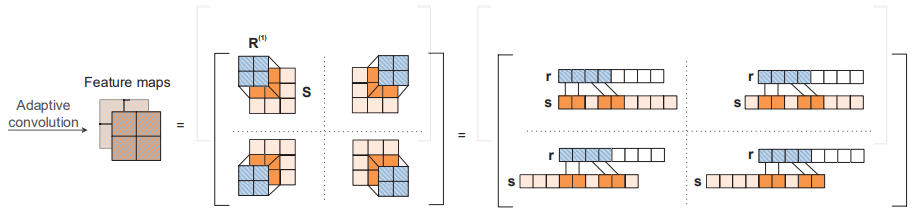  ConvR은 입력 \(\text{S}\)에 관계로 이뤄진 필터를 사용해 convolution 연산을 실행한다. 각각의 필터 \(\text{R}^{(l)}\)에 대해 convolution feature map \(\text{C}^{(l)}\in \Bbb R^{(d_e^h-h+1)\times(d_e^w-w+1)}\)을 생성한다. 그림 2는 convolution 연산을 통해 feature map이 생성되는 과정을 보여준다. adaptive convolution은 다양한 지역에서 입력 개체와 관계의 풍부한 상호작용을 가능하게 한다. 또한 생성된 모든 convolution feature는 이러한 상호작용을 가진다.
  마지막으로 트리플의 score\(\psi(s,r,o)\)를 계산하기 위해 convolution feature map \(\text{C}^{(1)},\dotsb,\text{C}^{(c)}\)를 쌓아 벡터 \(\text{c}\)를 만든다. 이 벡터는 \(\Bbb R^{d_e}\)로 이뤄진 fully connected layer에 prejected되고, 목적어 벡터 \(\text{o}\)에 match된다.
\(\psi(s,r,o)=f(\text{Wc+b})^\top\text{o}\),
\(\text{W}\in\Bbb R^{d_e\times c(d_e^h-h+1)\times(d_e^w-w+1)}, \ \text{b}\in \Bbb R^{d_e}\)는 fully connected layer의 parameter이고, \(f(\cdot)\)는 non-linear function이다.

Parameter learning

  모델의 parameter를 학습시키기 위해 ConvE 논문에서 소개된 1-N scoring을 사용했다. 1-N scoring은 \((s,r)\)을 입력으로 갖고 \(o\in \mathcal{E}\)인 모든 목적어 개체 후보에 대해 score vector \(\text{p}^{s,r}\in\Bbb R^{\mid\mathcal{E}\mid}\)를 생성한다. socre vector 각각의 차원은 목적어 개체에 대해 \(p^{s,r}_o = \sigma(\psi(s,r,o))\)를 계산한다. 입력 \((s,r)\)에 대해 cross-entropy loss를 최소화한다.
\(\mathcal{L}(s,r)=-\frac{1}{\mid\mathcal{E}\mid}\sum_{o\in\mathcal{E}}y_o^{s,r}\log{(p_o^{s,r})}+(1-y_o^{s,r})\log{(1-p_o^{s,r})}\)
\(y_o^{s,r}\)은 트리플이 참일 때 1, 거짓일 때 0이다. 최적화 과정에서 overfitting을 방지하기 위해 dropout을 적용했다. 또한 batch normalization, Adam optimizer, label smoothing을 사용했다.

Advantages over ConvE

  ConvE와 비교할 때 ConvR의 장점은 개체와 관계의 상호작용을 더 잘 포착할 수 있다는 점이다. ConvE는 개체와 관계의 concatenation line에서만 이러한 상호작용을 얻을 수 있고 이는 convolutional feature에서 아주 작은 부분에 해당한다. 반대로 ConvR은 개체와 관계의 다양한 지역에서 상호작용을 얻고, 모든 convolutional feature가 상호작용을 가진다.
  ConvR은 parameter 측면에서도 효율적이다. ConvE는 \(\mathcal{O}(d|\mathcal{E}|+d|\mathcal{R}|+chw+cd(2d^h-h+1)(d^w-w+1))\)의 공간 복잡도를 가진다. 여기서 \(chw\)는 \(h\times w\)를 크기를 갖는 \(c\)개의 global filter이고, \(d=d^hd^w\), \(cd(2d^h-h+1)(d^w-w+1)\)는 fully connected layer의 매개변수이다. 개체와 관계는 같은 크기 d를 가진다. ConvR은 \(\mathcal{O}(d|\mathcal{E}|+d|\mathcal{R}|+cd_e(d_e^h-h+1)(d_e^w-w+1))\)의 공간 복잡도를 가진다. ConvR은 global filter가 필요없다. 또한 convolution layer의 입력이 절반 크기이고 더 작은 feature map을 생성한다. 따라서 더 작은 fully connected layer를 가진다. 더 적은 parameter로 ConvE보다 ConvR이 더 좋은 성능을 보일 수 있음을 실험을 통해 보인다.

Experiments

Experimental Setup

Datasets

  실험을 위해 WN18, FB15k dataset과 역관계를 제거한 WN18RR, FB15k-237 dataset을 사용했다. 아래 표에 실험에 사용한 dataset의 상태를 요약했다.

Dataset	# Rel	# Ent	# Train	# Valid	# Test
FB15k	1,345	14,951	483,142	50,000	59,071
WN18	18	40,943	141,442	5,000	5,000
FB15k-237	237	14,541	272,115	17,535	20,466
WN18RR	11	40,943	86,835	3,034	3,134

Evaluation protocol

  각각의 트리플\((s,r,o)\)에서 주어 개체의 자리에 모든 개체\(e\in\mathcla{E}\)를 넣어 각각의 트리플 \((e,r,o)\)의 점수를 구한다. 점수 순으로 정렬한 뒤 참 트리플 \((s,r,o)\)의 순위를 구한다. 평가에 filtered setting 을 사용한다. filtered setting에 관한 설명은 ConvE 논문 리뷰에서 설명하였기 때문에 생략한다. 목적어 개체를 대체하는 경우에도 이 과정을 반복한다. 평가 항목으로는 MRR, Hits@n을 사용했다.

Implementation details

  ConvR 모델의 mini-batch size = 128, intial learning reate = 0.001, label smoothing coefficient = 0.1로 설정하였다. 다른 hyperparameter는 validation set의 MRR에 대한 grid search를 통해 결정하였다. Grid search에 사용된 Hyperparameter의 범위는 다음과 같다.

Hyperparameter	Range
entity embedding size	100, 200
filter number	0.0, 0.1, 0.2
filter size	0.0, 0.1, 0.2, 0.3
All dropout	0.1, 0.2, 0.3, 0.4, 0.5

Link Prediction Results

  아래 그림에 ConvR 모델의 실험 결과를 나타내었다.
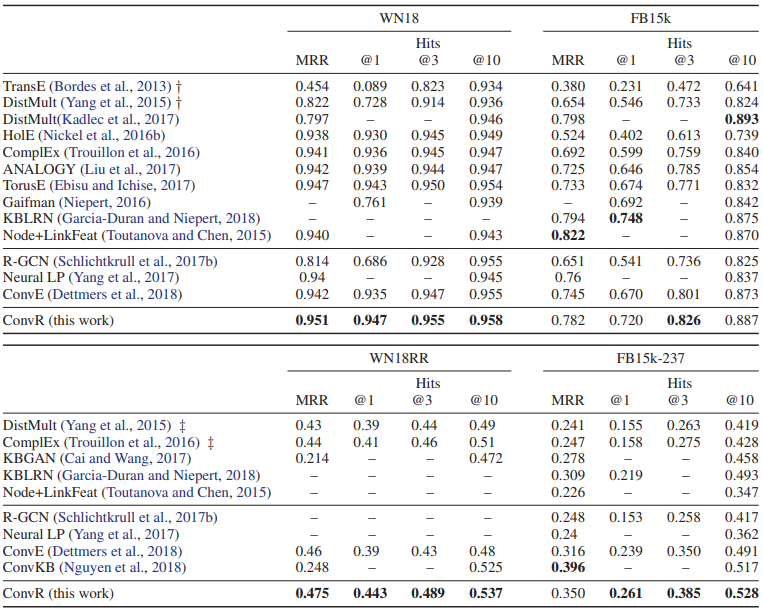대부분의 평가항목에서 가장 좋은 성능을 보였다.

Parameter Efficiency of ConvR

  FB15k-237에 대해 ConvR과 ConvE의 parameter 효율성을 비교해보았다. ConvR의 다른 hyperparameter는 각각의 최적 구정으로 사용하였고 필터의 숫자와 크기만 변경하여 실험하였다. 아래 그림에 parameter 수의 변화에 따른 ConvR 성능을 표현하였다.
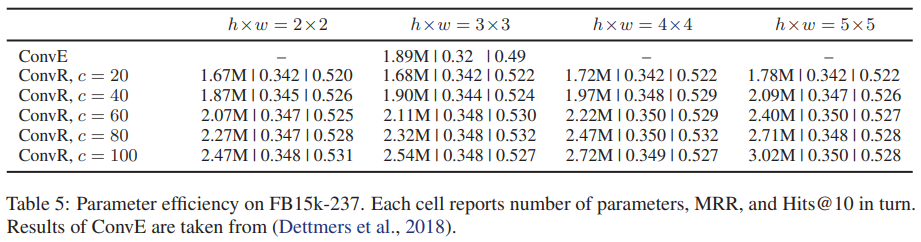실험 결과 ConvR parameter 수의 변화에 따른 성능의 차이는 크지 않았다. 그 의미는 ConvR이 적은 수의 parameter를 사용하더라도 좋은 성능을 낼 수 있다는 것을 의미한다. ConvR은 항상 ConvE보다 좋은 성능을 보였다. 특히 가장 작은 수의 parameter를 사용하였을 때에도 ConvE보다 좋은 성능을 보였다.

Conclusion

  ConvR은 adaptive convolution을 사용한 신경망이다. adaptive convolution은 다양한 지역에서 개체와 관계의 풍부한 상호작용을 포착할 수 있도록 한다.   추후에는 목적어 개체의 상호작용까지 포착할 수 있는 convolution을 연구하고자 한다.