Convolutional 2D Knowledge Graph Embeddings 논문 리뷰

Convolutional 2D Knowledge Graph Embeddings

• ConvE 논문의 해석 및 정리입니다.
• relation prediction, link prediction, knowledge graph completion 등으로 불리는 task를 공부하며 읽은 첫 논문입니다.

Introduction

  지식그래프(Knowledge graphs)는 지식베이스(Knowledge bases)에서 관계(relation)를 edge로 개체(entity)를 node로 바꾸어 만든 것이다. 지식그래프는 search, analytics, recommendation, data integration에서 중요한 자원이다. 그러나 그래프의 link가 누락되어 있는 불완전성으로 인해 사용에 어려움이 있다. 예를 들어 DBpedia의 Freebase는 66%의 사람 개체의 출생지가 연결되어 있지 않다. 이러한 link의 누락을 식별하는 것을 link prediction이라 부른다. 지식그래프는 수백만개의 사실을 포함할 수 있다. 따라서 link predictor는 파라미터의 수와 컴퓨팅 비용을 현실적으로 관리하는 방식으로 확장해야한다.
  이러한 문제를 해결하기 위해 link prediction 모델은 주로 제한된 수의 매개변수를 사용하고, 임베딩 공간에서의 행렬 곱같은 간단한 연산으로 구성되었다. DistMult는 parameter당 하나의 feature를 생성하는 embedding parameter간의 3방향 상호작용이 특징이다. 빠르고 간단한 얕은 모델을 사용해 덜 표현적인 feature를 배우는 대신 큰 지식그래프로 확장할 수 있다.
  얕은 모델의 feature 수를 늘리는 방법(표현력을 높이는 방법)은 embedding 사이즈를 증가시키는 것뿐이다. 그러나 이러한 방법은 더 큰 지식그래프로 확장되지는 않는데, embedding parameter의 수는 그래프의 개체와 관계 수에 비례하기 때문이다. 예를 들어 DistMult와 같은 얕은 모델의 embedding 사이즈가 200이라 가정하고 Freebase에 적용하면 이것의 parameter 용량은 33GB이다. embedding 사이즈와 관계 없이 feature의 수를 늘리려면 feature의 여러 레이어를 사용해야한다. 그러나 feature가 완전연결 레이어로 이뤄진 이전의 다층 지식그래프 임베딩구조는 overfit되기 쉬웠다. 얕은 구조의 크기 조절 문제와 완전연결된 깊은 구조의 overfit문제를 해결하기 위해서는 parameter를 효율적으로 사용하고, Deep network로 구성된 빠른 연산자가 필요하다.
  컴퓨터비전에서 주로 사용되는 convolution 연산자는 위의 속성을 만족한다. 게다가 다층 convolution 신경망을 학습할때 overfitting을 제어할 수 있는 강력한 방법론이 존재한다.
  이 논문에서는 지식그래프에서 embedding위에서 2D convolution 연산을 사용해 지식그래프의 손실된 link를 예측하는 모델, ConvE를 소개한다. ConvE는 단일 convolution layer, embedding dimension에 대한 projection layer, 내부 product layer로 구성된 간단한 다층 convolution 구조이다.

• 간단하지만 경쟁력있는 2D convolutional link prediction 모델 ConvE를 소개한다.
• 3배 빠른 훈련과 300배 빠른 평가를 가능하게 하는 1-N scoring 기법 개발.
• parameter 효율적인 모델을 만듬, DistMult와 R-GCNs에 비해 각각 8배, 17배 적은 parameter로 FB15k-237에서 더 나은 점수를 달성.
• ConvE와 다른 얕은 모델간의 성능 차이가 indegre와 PageRank로 측정한 지식그래프의 복잡도에 비례하여 증가한다.
• 주로 사용되는 link prediction dataset의 inverse relation으로 인한 평가의 어려움을 조사하였고 inverse relation을 제거한 버전의 dataset을 소개하여 간단한 규칙 기반 모델로 해결할 수 없도록 함.
• ConvE와 이전에 제안된 모델을 위에서 소개한 dataset으로 평가한 결과 MRR에서 state-of-the-art를 달성

Related Work

  여러 link prediction 모델이 제안되었다. Translating Embedding 모델(TransE), Bilinear Diagonal 모델(DistMult)등. 본 논문의 모델과 가장 유사한 모델은 Holographic Embedding 모델(HolE)이다. HolE는 cross-correlation을 사용한다. 그러나 HolE는 비선형 feature의 여러 layer를 학습하지 않아서 이론적으로 ConvE보다 표현력이 떨어진다.   ConvE는 link prediction에서 2D convolutional layer를 사용한 최초의 모델이다. Graph Convolutional Networks(GCNs)는 convolution 연산자가 그래프의 locality 정보를 생성하기 위해 사용되었다. 그러나 GCN framework는 undirected 그래프에 한정되어 있고, 지식그래프는 directed 그래프이다.
  여러 convolutional 모델들이 여러 자연어처리 task 해결을 위해 사용되고 있다. 그러나 대부분의 연구들은 embedding 공간 안에서 단어의 순서와 같이 embedding의 시간적 순서에 작동하는 1D convolution을 사용한다. 이 논문에는 embedding에 대해 공간적으로 작용하는 2D convolution을 사용한다.

Number of Interactions for 1D vs 2D Convolutions

1D convolution 대신 2D convolution을 사용하면 embedding 사이의 추가 상호 작용 지점을 통해 모델의 표현성이 향상된다. 예를 들어 두개의 1D embedding을 concatenate 한다고 생각하자.
\((\begin{bmatrix}a & a & a \end{bmatrix};\begin{bmatrix}b & b & b \end{bmatrix}) = \begin{bmatrix}a & a & a & b & b & b\end{bmatrix}.\)
사이즈가 3인 필터를 사용하면 concatenation point에서 두 embedding의 상호작용을 모델링 할 수 있다.
  두개의 2D embedding을 concatenate 한다고 가정하면 다음과 같은 결과를 얻는다. \((\begin{bmatrix}a & a & a\\ a & a & a \end{bmatrix};\begin{bmatrix}b & b & b\\ b & b & b \end{bmatrix}) = \begin{bmatrix} a & a & a \\ a & a & a \\ b & b & b \\ b & b & b \end{bmatrix}.\)
사이즈가 3x3인 필터를 사용하면 concatenation line에서 두 embedding의 상호작용을 모델링 할 수 있다.
  다음과 같은 다른 패턴도 사용할 수 있다.
\(\begin{bmatrix}a & a & a \\ b & b & b\\ a & a & a \\ b & b & b\end{bmatrix}.\)
이 경우에는 2D convolution 연산자가 a, b 사이의 더 많은 상호작용을 모델링 할 수 있다. 따라서 2D convolution이 1D convolution 보다 더 많은 feature 상호작용을 추출할 수 있다.

Background

  knowledge graph \(\mathcal{G} = \left\{ \left(s,r,o\right) \right\}\subseteq\mathcal{E}\times\mathcal{R}\times\mathcal{E}\)는 관계 \(r\in\mathcal{R}\)와 트리플의 주어와 목적어로 표현되는 두 개체 \(s,o\in\mathcal{E}\)를 포함하는 트리플의 집합으로 공식화할 수 있다. 각각의 트리플 \(\left(s,r,o\right)\)은 개체 \(s\),\(o\) 사이의 관계 \(r\)을 나타낸다.
  link prediction은 scoring function \(\psi:\mathcal{E}\times\mathcal{R}\times\mathcal{E}\mapsto\Bbb R\)을 평가하는 포인트 단위 학습으로 형식화 될 수 있다. 주어진 입력 트리플 \(x=\left(s,r,o\right)\)과 그 점수\(\psi\left(x\right)\in\Bbb R\)는 \(x\)가 참일 가능성에 비례한다.

Neural Link Predictors

  Neural link prediction 모델은 encoding component와 scoring component를 포함하는 multi-layer neural network로 볼 수 있다. 입력 트리플 \(\left(s,r,o\right)\)이 주어지면 encoding component는 주어와 목적어 개체를 분산 embedding 표현 \(e_s,e_o\in\Bbb R^k\)으로 mapping 한다. scoring component에서는 두 개체 embedding이 \(\psi_r\) 함수에 의해 평가된다. 트리플의 점수는 \(\psi\left(s,r,o\right) = \psi_r\left(e_s,e_o\right)\in\Bbb R^k\)과 같이 정의된다.

Convolutional 2D Knowledge Graphs Embeddings

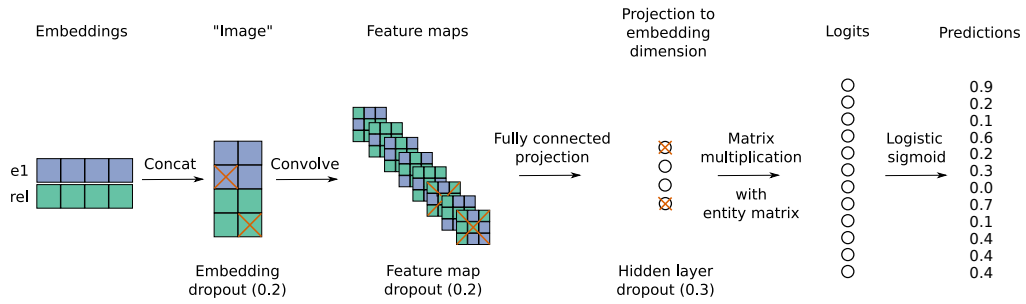
  이 연구에서는 convolution과 fully-connected layer로 구성된 neural link prediction 모델을 제안한다. 이 모델은 입력 개체와 관계 사이의 상호작용을 알아낸다. 2D embedding을 convolution 연산하여 score를 정의하는 것이 이 모델의 특징이다. 이 모델의 구조는 아래 그림과 같다.

그림1: 개체와 관계 embedding이 reshape, concatenate 된다.(step1,2); 그 행렬이 convolution layer에 입력으로 들어간다.(step3); 결과로 나온 feature map tensor는 k-차원 공간으로 vectorised, projected 된다.(step4); 목적어 embedding의 후보들과 match된다.(step5)

scoring function은 다음과 같이 정의된다.
\(\psi_r\left(e_s,e_o\right)\ =f(vec(f([\overline{e_s};\overline{r_r}]\ast \omega))W)e_o\)
\(r_r\in\Bbb R^k\)는 \(r\)의 관계 parameter이다. \(\overline{e_s},\overline{r_r}\)는 \(e_s,r_r\)의 2D reshape를 표현한 것이다. \(e_s,r_r\in\Bbb R^k\)이면 \(\overline{e_s},\overline{r_r}\in\Bbb R^{k_w\times k_h}\), \(k=k_w k_h\)이다.
  feed-forward pass에서 모델은 개체와 관계 두 embedding 행렬에 대한 row-vector look-up 연산을 수행한다. 모델은 \(\overline{e_s},\overline{r_r}\)를 concatenate하여 \(\omega\)를 필터로 갖는 2D convolution layer에 입력한다. 이 결과로 feature map tensor \(\mathcal{T}\in\Bbb R^{c\times m\times n}\), \(c,m,n\)은 각각 2D feature map의 수와 그 차원이다. tensor \(\mathcal{T}\)는 vector\(\ vec(\mathcal{T})\in\Bbb R^{cmn}\)로 reshape 된다. 행렬 \(W\in \Bbb R^{cmn\times k}\)로 선형변환되어 \(k\)차원의 공간으로 투영된다. 그 값은 목적어 embedding \(e_o\)와 내적으로 match 된다.
  모델의 parameter를 훈련시키기 위해서 score fucntion에 logistic sigmoid function을 적용하고, 아래의 binary cross entropy loss를 최소화하도록 하였다.
\(\mathcal{L}(p,t) = -\frac{1}{N}\sum_i(t_i\cdot \log{(p_i)}+(1-t_i)\cdot\log{(1-p_i)})\)
\(t\)는 1-1 scoring에서 \(\mathcal{R}^{1x1}\)차원 또는 1-N scoring에서 \(\mathcal{R}^{1xN}\) 차원을 가지는 label vector이다. vector \(t\)의 요소는 존재하는 관계에 대해서는 1이고 다른 경우에는 0이다.
  모델의 빠른 훈련을 위해 비선형 \(f\)에 대해 rectified linear units을 사용했다. 각 layer 마다 batch normalisation을 사용했다. dropout을 사용해 모델을 정규화했다. 특히 embedding, feature map, convolution 연산, fully connected layer 이후의 hidden units에 dropout을 적용했다. Adam optimiser를 사용했고, label smoothing을 사용했다.

Fast Evaluation for Link Prediction Tasks

  이 구조에서 convolution 연산은 전체 연산 시간의 75-90%을 차지한다. 따라서 전체 연산 시간을 줄이려면 convolution 연산의 수를 줄이는 것이 중요하다. link prediction 모델에서는 평가 속도를 높이기 위해 주로 batch size를 증가시킨다. 그러나 convolution 모델에서는 batch size를 늘리는데 필요한 메모리량이 GPU의 메모리 용량을 빠르게 넘어가기 때문에 적합하지 않다.
  ConvE는 다른 link prediction 모델과 같이 트리플\((s,r,o)\)로 1-1 scoring을 하는 대신, 하나의 \((s,r)\)쌍으로 모든 개체\(o\in \mathcal{E}\)에 대해 1-N scoring을 시행한다. convolution 모델의 평가에서 1-1 scoring과 1-N scoring은 약 300배의 시간 차이가 난다.

Experiments

Knowledge Graph Datasets

  ConvE의 평가를 위해 다음과 같은 dataset을 사용했다. +WN18 : 18개의 관계와 40,943개의 개체로 이뤄진 WordNet의 부분 집합, 151,442개의 트리플 대부분은 상위어와 하위어로 구성되어 있어 계층적인 구조이다. +FB15k : 1,345개의 관계와 14,951개의 개체로 이뤄진 Freebase의 부분 집합, 이 그래프는 영화, 배우, 상, 스포츠, 스포츠 팀에 대한 설명으로 이뤄짐. +YAGO3-10 : 37개의 관계와 123,182개의 개체로 이뤄진 YAGO3의 부분 집합, 각각 최소 10개의 관계를 갖는 개체로 구성됨. +Countries   WN18과 FB15k는 역관계(inverse relation)으로 인해 test에 문제가 있다. training set의 트리플을 반전시킴으로써 간단히 많은 양의 test triple을 얻을 수 있다는 점이다. 예를 들어 test set에 존재하는 (s, 하위어, o)인 트리플을 반전시킨 (o, 상위어, s)인 트리플이 training set에 있는 경우가 많다.
  논문에서는 간단한 룰 기반의 모델을 만들어 WN18과 FB15k에서 state-of-the-art 결과를 보임으로 이 문제를 제기하였다. 역관계로 인한 test의 오류가 없는 것을 증명하기 위해 FB15k에서 역관계를 제거한 FB15k-237과 WN18에서 역관계를 제거한 WN18RR에 룰 기반 모델을 적용했다. 이 논문에서는 앞으로의 연구에서 FB15k와 WN18 대신 YAGO3-10, FB15k-237과 WN18RR을 사용하는 것을 권장한다.

Experimental Setup

  Validation set의 MRR에 대한 grid search를 통해 ConvE의 hyperparameter를 선택하였다. Grid search에 사용된 Hyperparameter의 범위는 다음과 같다.

Hyperparameter	Range
embedding dropout	0.0, 0.1, 0.2
feature map dropout	0.0, 0.1, 0.2, 0.3
projection layer dropout	0.0, 0.1, 0.3, 0.5
embedding size	100, 200
batch size	64, 128, 256
learning rate	0.001, 0.003
label smoothing	0.0, 0.1, 0.2, 0.3

  Hyperparameter에 대한 grid search외에도 2D Convolution layer를 fully connected layer 또는 1D convolution으로 대체하는 실험도 진행하였다. 그러나 이러한 실험 결과는 좋지 않았다. 또한 필터의 크기를 달리한 실험도 진행하였다. 결과적으로 작은 크기(3x3)의 필터를 사용하는 경우에 좋은 결과를 얻었다.

Inverse Model

  WN18과 FB15k의 94%와 81%의 트리플이 test set과 연결된 역관계 트리플을 갖고 있다. 즉 두 사이의 관계가 역관계라는 것을 알면 test 트리플을 쉽게 training 트리플로 mapping 할 수 있다는 뜻이다. 예를 들어 상위어와 하위어가 역관계라는 것을 알면 (토끼, 상위어, 동물)로부터 (동물, 하위어, 토끼)를 쉽게 얻을 수 있다. link prediction 모델이 어떠한 관계가 다른 것과 역관계인지 알면 쉽게 예측을 할 수 있기 때문에 문제가 된다.
  이 논문에서는 두 관계 쌍\(r_1,r_2 \in \mathcal(R)\)에 대해 \((s,r_1,o)\)와 \((o,r_2,s)\)를 만족하는지 확인하는 간단한 inverse model을 만들었다.
  실험에서 test 트리플의 역관계 트리플이 test set 바깥에서 확인되면 매치된 k개에 대한 상위 k개의 순위 순열을 샘플링한다. 발견되지 않으면 랜덤으로 test 트리플에 대한 순위를 선택한다.

Results

  이전의 연구들과 같이 filtered setting을 사용하여 실험을 진행하였다. link prediction의 평가는 test set에 속한 트리플의 한 개체를 지우고 빈 자리에 가능한 모든 후보 개체를 대입하여 그 중 정답의 순위를 매기는 방식이다. 이 방식의 문제는 복수의 정답이 생길 가능성이 있다는 것이다. 예를 들어 (윤종신, 부른 노래, 좋니)라는 트리플에서 평가를 위해 목적어 개체 ‘좋니’를 지운 후 개체의 후보군을 대입한다. 이 경우 (윤종신, 부른 노래, )는 ‘좋니’, ‘오르막길’, ‘나이’ 등 복수의 정답을 가질 수 있다. filtered setting은 이 문제를 해결하기 위해 개체의 후보군을 대입한 트리플이 기존의 training, validation, test set에 존재하는 경우 삭제하여 준다. 위의 예에서는 정답인 ‘좋니’를 제외한 다른 정답 ‘오르막길’, ‘나이’ 등의 개체는 후보 개체에서 제외되는 것이다.
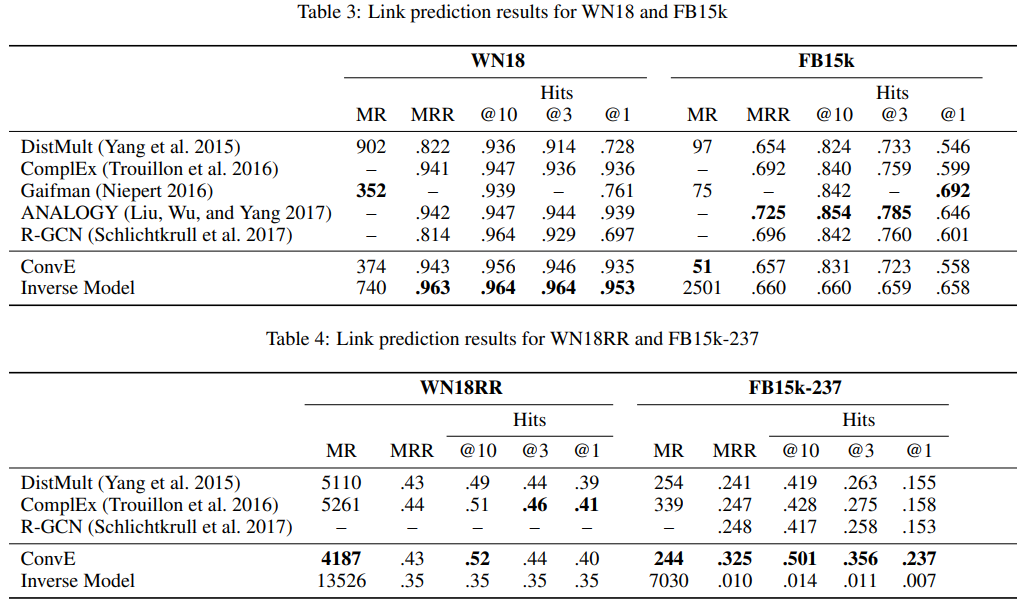
FB15k, WN18, FB15k-237, WN18RR에 대한 실험 결과는 다음과 같다.
YAGO3-10과 Countries에 대한 결과는 다음과 같다.
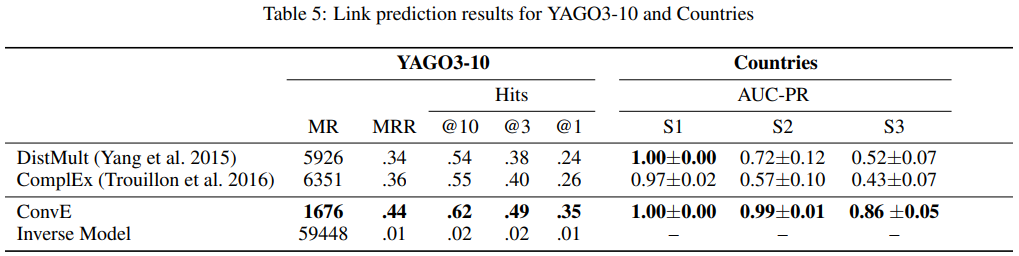
  inverse model은 FB15k와 WN18의 많은 측정 항목에서 state-of-the-art 성능을 가졌다. 그러나 YAGO3-10과 FB15k-237 dataset에서는 역관계를 추출하지 못하였다. FB15k-237을 만드는 과정에서 ‘similar to’와 같은 대칭적인 관계는 제거하지 않았다. 이러한 관계가 존재한다는 점은 동일한 과정을 거쳐 만들어진 WN18RR에서 inverse model이 좋은 점수를 가지는 이유가 된다.

Parameter efficiency of ConvE

  ConvE는 FB15k-237에서 0.23M개의 parameter로 1.89M개의 parameter를 쓰는 DistMult보다 좋은 성능을 보였다. ConvE는 0.46M개의 parameter로 FB15k-237의 Hits@10에서 0.425로 state-of-the-art를 달성했다. 이전의 가장 좋은 모델 R-GCN은 동일 항목에서 8M개의 parameter로 0.417을 기록하였다. ConvE는 R-GCN 보다 17배, DistMult보다 8배 좋은 parameter 효율을 보인다. Freebase 전체에서 모델의 크기는 R-GCN의 경우 82GB, DistMult의 경우 21GB로 ConvE의 5.2GB보다 크다.

Analysis

Ablation Study

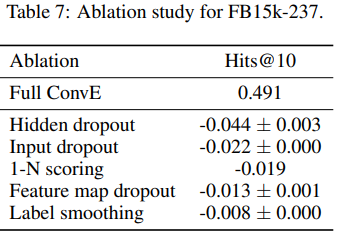
  위 그림은 ablation study의 결과를 나타낸다. Hidden dropout이 가장 중요한 요소란 것을 알 수 있다. 1-N scoring도 성능 향상에 영향을 준다. Label smoothing은 성능에 큰 영향을 주지 않는다.

Analysis of Indegree and PageRank

  ConvE는 WN18RR보다 YAGO3-10, FB15k-237에서 더 좋은 성능을 보인다. 이에 대해 논문에서는 두 dataset의 node가 WN18RR에 비해 굉장히 높은 relation-specific indegree를 갖기 때문이라고 주장했다. 예를 들어 head node “US”는 edge “was born in”에서 10,000개 이상의 진입차수를 갖는다. “US”로 향하는 tail node들은 배우, 작가, 학자, 사업가 등으로 아주 다양하다. 진입차수를 많이 갖는 head node를 성공적으로 모델링하기 위해서는 연결되는 tail node의 다양한 특징을 성공적으로 포착할 수 있어야 한다. 이 논문은 여러 layer의 feature를 학습하는 깊은(deep) 모델(ConvE)일수록 얕은 모델(DistMult)보다 이러한 특징을 포착하는데 유리하다고 주장한다.
  그러나 깊은 모델일수록 최적화가 어렵다. 이에 대해 논문은 WN18이나 WN18RR 같은 낮은 relation-specific indegree를 갖는 dataset에서는 DistMult 같은 얕은 모델이 더 정확할 수 있다고 주장했다.
  두 주장이 옳음을 실험하기 위해 relation-specific indegree이 높은 FB15k, 낮은 WN18을 사용했다. 또한 각각의 dataset에서 높거나 낮은 indgree node를 삭제하여 relation-specific indegree가 낮은 low-FB15k, 높은 high-WN18 dataset을 만들었다. 실험에 DistMult와 ConvE 모델을 사용했다. 논문의 가설이 맞다면 높은 relation-specific indegree를 갖는 dataset에서 ConvE는 DistMult보다 항상 좋은 결과를 가질 것이다.
  실험의 평가 항목으로 hits@10을 사용했다.

dataset	ConvE	DistMult
FB15k	0.831	0.824
high-WN18	0.952	0.938
low-FB15k	0.586	0.728
WN18	0.956	0.936

실험 결과 깊은 모델은 복잡한 그래프에서 좋은 성능을 보이고, 얕은 모델은 간단한 그래프에서 좋은 성능을 보였다.
  이를 자세히 조사하기 위해 node의 중심성을 측정하는 PageRank를 사용했다. PageRank는 node의 recursive indegree를 측정한다. node의 PageRank값은 node, node의 이웃, node의 이웃의 이웃의 indegree 등, network의 다른 모든 node에 비례한다. 이러한 이유로 ConvE는 PageRank의 평균이 높은 dataset에서 좋은 성능을 보일 것이다.
  이를 증명하기 위해 각각의 dataset에 대한 PageRank를 측정하였다.

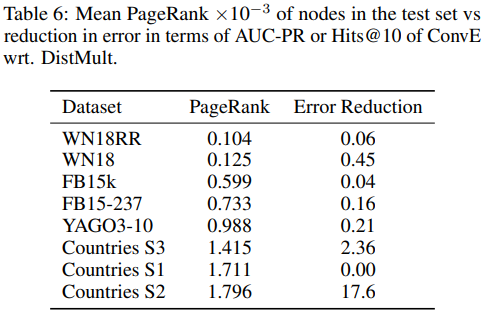
위 그림은 test set에 포함된 node의 PageRank 평균과 Hits@10에 대한 DistMult와 ConvE의 성능 차이를 나타낸다. 이러한 증거들로 깊은 모델이 relation-specific indegree가 높은 dataset에 대해 유리하다는 것을 증명할 수 있다.

Conclusion and Future Work

  ConvE는 link prediction에서 2D convolution을 사용한 최초의 모델이다. 기존 모델에 비해 적은 parameter를 사용해 좋은 성능을 보였고, 1-N scoring을 통해 속도를 향상시켰다. WN18과 FB15k에서 역관계 문제를 지적하였고, 이를 해결한 dataset을 소개하였다.
  ConvE는 컴퓨터 비전에 사용되는 다른 구조와 비교하였을때 얕은 편이다. 추후에는 convolution 모델을 더 깊게 만들려 한다. 또한 embedding 공간에 대규모 구조를 적용해 embedding 간 상호 작용의 횟수를 늘리려 한다.